Unpinning Spiral Waves Using Circularly Polarised Electric Fields

Spiral waves have been found in a variety of human organs like the surface of the retina causing migraine, inside the brain fostering epilepsy and in the heart muscle leading to fatal cardiac arrhythmias. In many physiological tissues, such rotating waves of activity are pathological, and in heart, it leads to cardiac rhythm disorders or even fatal conditions such as ventricular fibrillation. Thus in many situations, it is desirable to remove such spiral waves from the medium.

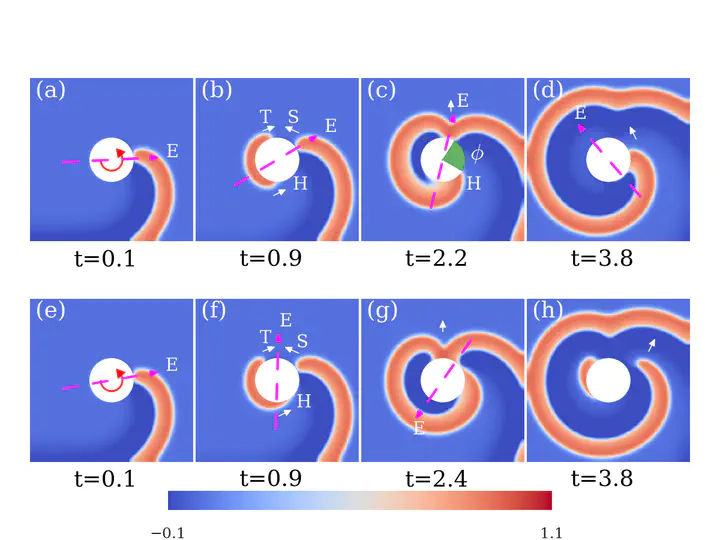
However, in heterogeneous media, rotating spiral waves tend to move towards heterogeneities (henceforth called obstacles) in the medium and rotate around the boundary of the obstacle as if the wave is pinned to it. Unpinning a pinned wave requires a careful stimulus given close to the core of the pinned wave and within a short time interval known as the unpinning window of the spiral wave. One method of eliminating these spirals are by using multiple periodic field pulses. The idea here is to shoot multiple pulses at the rotating spiral and hope that one pulse falls into the unpinning window and eliminates the pinned spiral. However, there is a problem with this approach. If the unpinning window is quite narrow, the chances of pulses delivered falling into the unpinning window are very less. To circumvent the problem, we use circularly polarised electric fields instead of traditional dc field pulses.

In this project, we present a mechanism for unpinning the spiral waves using circularly polarised electric fields. We show that for a given obstacle size, there exists a time period of the CPEF below which spiral can always be unpinned. We call it the cut-off time period. We also show that the termination always happens within the first period of the CPEF. We derive a robust and generalised analytical formulation which explains the findings of the simulations. Our theory accurately predicts the cut-off time period of CPEF. In particular, we show that unpinning is always successful if the period of the CPEF is below the cut-off period. We also show that the cut-off period depends linearly on the radius of the obstacle. We find that there is no traditional unpinning window with the circularly polarised electric field.